数学ど素人ですが、RSA 暗号で利用する数学的知識や計算方法について勉強しました。
当然ですが、素人の解説なので正しいかどうかも不明です。
今までエンジニアとして仕事をしてきまして、公開鍵暗号化方式の仕組みは理解していますが、暗号化・復号の数学的な計算方法がさっぱり分かりませんでした。
暗号技術の本を読むと、「素数」とか「素因数分解」とか「オイラーのなんとか」…など、全く理解できないのが悔しく思っていました。(結局ページを飛ばして読んだ気になる)
エンジニアなので(?)、仕事が終わった後も勉強しようと思い、Kindle で暗号関係の本を購入しましたが
読んでもさっぱり理解ができていませんでした。
しかし、とうとう一念発起して勉強することとしました。
本記事は勉強したことのまとめと復習用に作成しました。
そのため、ところどころ重複していたり、あいまいな点があるかもしれませんがご容赦ください。
正直に言いますと、ネットで数多くの数学解説サイトがありますが、難しすぎるといいますか、レベルが高すぎてついていけませんでした。
もっとレベルを下げて解説していただけると大変うれしいですね。
と言っても本来なら本を購入して勉強するのが正しいですが。
今回勉強させていただいた動画
以下の Youtube の解説を中心に勉強させていただきました。
ありがとうございます。
第1回 余りつき割り算
第2回 合同式の計算方法
第3回 合同式の演習
第4回 ユークリッドの互除法と一次不定方程式
第5回 合同式の重要性質2(乗法単元)
第6回 中国剰余定理
第7回 フェルマーの小定理
第8回 RSA暗号の仕組み解説
第9回 RSA暗号の仕組み[証明]
RSA 暗号を理解しようとすると以下の数学的知識が必要になる
RSA 暗号を理解しようとすると以下の数学的知識が必要になります。
- 最大公約数の計算
- 整数の合同
- ユークリッドの互除法
- オイラー関数
- フェルマーの小定理
- 素数、素因数分解
個人的には「ユークリッドの互除法」がよく分かりませんでした。
以下、最初に数学の勉強をしてから、最後に勉強した数学の知識を利用して RSA 暗号の計算を試してみます。
また、冗長になりますが、具体的に数字を入れて何度か計算を試しています。例をたくさん入れることで私も含めて初心者にも分かりやすくなると思います。
RSA とは
そのそも RSA とは何でしょうか。
RSA とは、公開鍵暗号方式のアルゴリズムの 1 つです。(ということは RSA 以外にも公開鍵暗号方式のアルゴリズムがあります)
RSA は3人の開発者の頭文字を取っています。
- R ← Ron Rivest(ロン・リヴェスト)
- S ← Adi Shamir(アディ・シャミア)
- A ← Leonard Adleman(レナード・アドルマン)
RSA による暗号化の式
暗号文 = 平文^e mod n
つまり、暗号化とは、「暗号文を数字化して(例えば ASCII コードなら 1文字 1文字に番号が付いています)、それを e 乗して n で mod を取ったもの(余りを出したもの)」です。
後ほど詳しく解説しますが、この e と n が公開鍵になります。
つまり、メッセージを送りたい A さんが、B さんよりこの公開鍵をもらって、この公開鍵で暗号化して送信します。
この e と n はどんな数字でもいいのかというと、いろいろな条件がありますが、それをこれから勉強します。
【例】
例えば、
e = 7
n = 33
として
メッセージを ASCII コード化した番号が「65」の場合は、以下のようになります。
65^7 ÷ 33 の余りは以下のようになります。
4,902,227,890,625 mod 33 = 32
RSA による復号の式
平文 = 暗号文^d mod n
暗号化の式とほぼ一緒です。
e と d が変わっただけです。
ただ、d の出し方は複雑です。
公開鍵と秘密鍵を使って暗号化したり復号していますが、それをこれから解説します。
最大公約数の計算
最大公約数は勘違いしなければ簡単です。
- 約数 ← 割り切れる数
- 公約数 ← 複数の数字で共通して割り切れる数
【例】
28 と 42 の最大公約数は?
- 28 の約数 ← 1, 2, 4, 7, 14, 28
- 42 の約数 ← 1, 2, 3, 6, 7, 14, 42
14 だけでなく 1 や 2 や 7 も共通していますが、その中で「最大」なのが 14 です。
その結果、28 と 42 の最大公約数は 14 になります。
最大公約数は、複数の数より共通の約数で且つその中で最大の約数を見つけます。
整数の合同(合同式)
整数の合同とは、2 つの整数の間に認められる関係です。
関係を「法」で表します。
「法」は「ほう」と読むようです。
※数学用語は音読みがほとんどのようです。
RSA 暗号での計算としては、「合同式」が使われます。
数学を解説しているサイトを見ると、アナログ時計を例として「余りの考え方」を説明されることが多いようです。
例えば、アナログ時計は 12 時に到達するたびに 0 になります。このことを法 12 と言います。
整数の合同の定義
「2 つの整数 a,b が法 n に対して合同」という言い方をします。
例えば、アナログ時計の場合、1 時と 13 時は、「法 12 に対して合同」になります。
2つの整数が同号であることを表示するのに、合同式を使い、「≡」という記号を使います。
パソコンの場合は、「ごうどう」と入力すると、候補に「≡」の記号が表示されます。
上のアナログ時計の例ですが、違う表現としては「a を n で割った余りと、b を n で割った余りが同じ」という言い方をします。
1 を 12 で割った余り(1)と 13 を 12 で割った余り(1)は同じです。
- 1時 ← 時計の針の位置は 1
- 13時 ← 時計の針の位置は 1
- 25時 ← 時計の針の位置は 1
この「法」について考えると、IT エンジニアならすぐに気が付くかと思いますが、「2進数」とか「8進数」とか「10進数」などの考え方と同じだなと思いました。
例えば、アナログ時計で言えば「12進数」になると思います。
合同式を表現すると以下のようになります。
a ≡ b(mod m)
2 つの整数 a,b が法 m に対して合同である。
【例】
1 ≡ 13(mod 12)
2 つの整数 1, 13 は法 12 に対して合同である。
別の表現方法だと、「a を m で割った余りと、b を m で割った余りが同じ」になります。
【例】
13 ≡ 1(mod 12)
法 12 において、13 と 1 は合同である。
12進数の世界では、13 と 1 は同じである。
【例】
17 ≡ 32(mod 15)
法 15 において、17 と 32 は合同である。
15進数の世界では、17 と 32 は同じである。
【例】
16 ≡ 1(mod 15)
法 16 において、16 と 1 は合同である。
15進数の世界では、16 と 1 は同じである。
【例】
a が 22
b が 17 の場合、
n を 5 にする(法 5)と合同式が成り立ちます。
a ≡ b(mod m)
22 ≡ 17(mod 5)
22 も 17 もどちらも余りは 2 になります。
【例】
- 22 ÷ 5 = 4 余り 2
- 17 ÷ 5 = 3 余り 2
ちなみに、合同式に 2 は出てきません。
法(ほう)とは何か一言でというと、割る数のことを言います。
コンピュータの世界では「基数」が「5」という言い方になります。
例えば、2進数の場合は、基数が 2 になります。
先ほどのアナログ時計の例では「12」で割っているので、法は「12」になります。
基数が 12 の 12進数という言い方もできます。
※余りのことを剰余(じょうよ)ということもあります。要するに割り算の余りのことです。
※剰余演算をモジュロと言います。
また、以下のように整数 a と b が m で割った余りが同じ場合
a ≡ b(mod m)
a – b は m の倍数となります。
【例】
22 ≡ 17(mod 5)
22 – 17 = 5
5 は 5 の倍数です。
【例】
1 ≡ 13(mod 12)
1 – 13 = -12
-12 は 12 の倍数です。
その理由は、左辺引く右辺でお互いに余りを相殺しているからです。
また、以下のようになります。
- a ≡ c(mod m)
- b ≡ d(mod m)
の場合、
- a + b ≡ c + d(mod m) a と b を足した数字と c と d を足した数字も m で割った数は等しい。
- a – b ≡ c – d(mod m) a から b を引いた数字と c から d を引いた数字も m で割った数は等しい。
- ab ≡ cd(mod m) a と b を掛けた数字と c と d を掛けた数字も m で割った数は等しい。
- a^n ≡ b^n(mod m) a の n 乗と b の n 乗も m で割った数は等しい。
↓
aⁿ ≡ bⁿ(mod m) ※n は自然数
例(足し算の場合)
22 ≡ 17(mod 5)
18 ≡ 13(mod 5)
↓
22 + 18 ≡ 17 + 13(mod 5)
↓
40 ≡ 30(mod 5)
mod とは
mod は「モッド」と読みます。
mod は「割り算をして余りを求める」ための式で使います。
【例】
- 27 mod 12 = 3 ← 27 を 12 で割ると 3 が余る。
- 36 mod 12 = 0 ← 36 を 12 で割ったが余りがなかった。
- 8 mod 12 = 8 ← 8 を 12 で割ったが、割れなかった(0)ので、余りが 8 になった。
この数値が仮に大きな数になっても、Windows の関数電卓があれば簡単に計算ができます。
【例】
15^31 mod 12 = 3
Windows の関数電卓を使って簡単に 3 を出せました。
- 15^31 ← 15 の 31 乗です。
ユークリッドの互除法
ユークリッドの互除法とは、2つの自然数の最大公約数を求める手法の1つです。
- 互除法(ごじょほう) ← 割り切れるまでお互いを割り続けるという意味です。
例(219 と 69 の最大公約数を求める方法)
219 = 69 × 3 + 12 ← 219 を 69 で割る。69 × 3 で 207 になり、余りは 12 となる。
↓
69 = 12 × 5 + 9 ← 次は、割った数 69 と余りの数 12 を使って計算する。69 を 12 で割る。12 × 5 で 60 になり、余りは 9 となる。
↓
12 = 9 × 1 + 3 ← 次は、割った数 12 と余りの数 9 を使って計算する。12 を 9 で割る。9 × 1 で 9 になり、余りは 3 となる。
↓
9 = 3 × 3 + 0 ← 次は、割った数 9 と余りの数 3 を使って計算する。9 を 3 で割る。3 × 3 で 9 になり、余りは 0 となる。
以上の結果により、219 と 69 の最大公約数は「3」となります。
これは以下のように表現できます。
GCD(219, 69) = 3
※GCD は Greatest Common Divisor の略で最大公約数のことを言います。
また、x と y を使うと、以下のように表現できます。
219x + 69y = 3
ここから x と y を導き出すのが難しいです。
もっと数字が小さい場合は、暗算で何となく x と y を見つけることができます。
x と y を導き出すには上で利用した式を利用します。
私も最初はなんのこっちゃかさっぱり分かりませんでした。
上の式
① 219 = 69 × 3 + 12
↓
② 69 = 12 × 5 + 9
↓
③ 12 = 9 × 1 + 3
↓
④ 9 = 3 × 3 + 0
この 4 つの式を逆にしていきます。
3 を導き出します。
3 = 12 – 9 ← これは③の 12 = 9 × 1 + 3 を利用しています。
3 を 左辺にもっていき、12 を右辺にもっていきます。
次に、3 = 12 – 9 の 9 に着目します。
この 9 の部分に②の式を入れます。
②の式の 12 × 5 を左辺にもっていき、69 – (12 × 5) = 9 の形にして、
3 = 12 – 9 の 9 の部分に入れます。
そうすると、以下のようになります。
3 = 12 – (69 – 12 × 5)
上の式を見ると、12 が重複しています。
12 × 5 をカッコから出すと、以下のようになります。
3 = 12 × 6 – 69
次に①の式の 12 に着目します。
この 12 を 3 = 12 × 6 – 69 の 12 に入れます。
①の式を変えると以下のようになります。
219 – 69 × 3 = 12
これを 3 = 12 × 6 – 69 の 12 に入れます。
3 = (219 – 69 × 3) × 6 – 69
これを整理すると、219 × 6 – 69 × 18 – 69
3 = 219 × 6 – 69 × 19
になります。
ここから、219x + 69y = 3 は、
(x, y) = (6, -19) となります。
※正直言うと、なぜこうなるのか、なぜこういう計算をしているのかがよく分かりません。
参考
第4回 ユークリッドの互除法と一次不定方程式
更にユークリッドの互除法の解説をします。
2つの自然数 a,b について、a を b で割った時の商を q, 余りを r とすると
a = bq + r になります。
- 自然数 ← 正の整数のことを言います。
- 自然数の例:1,2,3,4,100,333,11111 など
- 間違い例:-1, -2, 6.5
また、
GCD(a,b) = GCD(b,r) ← a と b の最大公約数と b と r の最大公約数は同じということです。
になります。
例えば
GCD(50,3)の場合、
50 = 3 × q + r になります。
q と r を計算すると、
50 = 3 × 16 + 2
になります。
ここから、
GCD(50,3) = GCD(3,2)
になります。
互いに素とは、2つの整数の公約数が「1」のみであることを言います。
例えば、2つの整数が 2 と 5 の場合は、公約数が「1」のみであると言えます。
ちなみに、8の約数は 1,2,4,8 です。
例えば、2つの整数(5,15)の場合は、公約数は 1,5 になります。
- 約数 ← 1つの整数に対して使う
- 公約数 ← 複数の整数の約数に対して使う
法が 12 の場合の 互いに素 とは
- 互いに素 ← 最大公約数が 1 のみの整数
【例】 法 12 の場合の互いに素
- 1 mod 12 = 1 → 〇(存在する)【最大公約数は 1】
- 2 mod 12 = 1 → ×(存在しない)2 と 12 は 12 で割り切れる
- 3 mod 12 = 1 → ×(存在しない)3 と 12 は 3 で割り切れる
- 4 mod 12 = 1 → ×(存在しない)4 と 12 は 4 で割り切れる
- 5 mod 12 = 1 → 〇(存在する)【最大公約数は 1】
- 6 mod 12 = 1 → ×(存在しない)6 と 12 は 6 で割り切れる
- 7 mod 12 = 1 → 〇(存在する)【最大公約数は 1】
- 8 mod 12 = 1 → ×(存在しない)8 と 12 は 2,4 で割り切れる
- 9 mod 12 = 1 → ×(存在しない)9 と 12 は 3 で割り切れる
- 10 mod 12 = 1 → ×(存在しない)10 と 12 は 2 で割り切れる
- 11 mod 12 = 1 → 〇(存在する)【最大公約数は 1】
- 12 mod 12 = 1 → ×(存在しない)12 と 12 は 12 で割り切れる
- 13 mod 12 = 1 → 〇(存在する)【最大公約数は 1】
- 14 mod 12 = 1 → ×(存在しない)14 と 12 は 2 で割り切れる
- 15 mod 12 = 1 → ×(存在しない)15 と 12 は 3 で割り切れる
- 16 mod 12 = 1 → ×(存在しない)16 と 12 は 2,4 で割り切れる
- 17 mod 12 = 1 → 〇(存在する)【最大公約数は 1】
- 18 mod 12 = 1 → ×(存在しない)18 と 12 は 2 で割り切れる
上記のように最大公約数が 1 のみである整数があります。
10進数的には素数ではありませんが(2 と 3 が当てはまらないため)、12進数的には素数となります。
- 素数 ← 1 より大きい自然数(正の整数)で、正の約数が 1 と自分自身のみであるもののことを言います。
一次不定方程式とは
- 不定方程式 ← 解(かい、答えのこと)が無数にある方程式のことを言います。
- 一次 ← 式に出てくる x や y が 1 乗であること
- 二次 ← 式に出てくる x や y が 2 乗であること(x² や y² など)
- 三次 ← 式に出てくる x や y が 3 乗であること(x³ や y³ など)
つまり一次不定式とは、x や y が 1 乗で且つ答えが無数にある方程式のことを言います。
【式】
ax + by = 1
- a と b は整数
- a と b は互いに素
互いに素とは、2つの整数の公約数が「1」のみであることを言います。
例えば、2つの整数が 2 と 5 の場合は、公約数が「1」のみであると言えます。
【例】
5x + 7y = 1
例えば、
x が 3
y が -2
の場合、
5 × 3 + 7 ×(-2) = 15 – 14 = 1
になります。
オイラーの定理(オイラー関数)
オイラーの定理、またはオイラー関数です。
- オイラー ← レオンハルド・オイラー(1707~1783)数学者、天文学者
- オイラー関数 ← φ(n)
※φの記号は ファイ と入力すると変換候補としてできてます。
オイラー関数 φ(n) の説明
n が正整数(プラスの整数)の場合、1 から n までの整数で、n と互いに素となるものの個数を φ(n) で表します。
互いに素とは、2つの整数の公約数が「1」のみであることを言います。
例えば、2つの整数が 2 と 5 の場合は、公約数が「1」のみであると言えます。
【例】
- GCD(2,5)=1 ← 2つの整数が 2 と 5 の場合
- GCD(3,10)=1 ← 2つの整数が 3 と 10 の場合
- GCD(3,6)=3 ← 3 と 6 の場合は、最大公約数(Greatest Common Divisor)は 3 になるので、1 ではありません。
【例】
- φ(1) = 1
- φ(2) = 1
- φ(3) = 2 ← 1 と 2 が 3 と互いに素
- φ(4) = 2 ← 1 と 3 が 4 と互いに素
- φ(5) = 4 ← 1 と 2 と 3 と 4 が 5 と互いに素
- φ(6) = 2 ← 1 と 5 が 6 と互いに素
- φ(7) = 6 ← 1 と 2 と 3 と 4 と 5 と 6 が 7 と互いに素
- φ(8) = 4 ← 1 と 3 と 5 と 7 が 8 と互いに素
- φ(9) = 6 ← 1 と 2 と 4 と 5 と 7 と 8 が 9 と互いに素
- φ(10) = 5 ← 1 と 3 と 4 と 7 と 9 が 10 と互いに素
- φ(11) = 10 ← 1 と 2 と 3 と 4 と 5 と 6 と 7 と 8 と 9 と 10 が 11 と互いに素
ちなみに Wikipedia に素数一覧が掲載されています。
https://ja.wikipedia.org/wiki/%E7%B4%A0%E6%95%B0%E3%81%AE%E4%B8%80%E8%A6%A7
ここで素数の 5 と 7 に注目すると、
- φ(5) = 4 ← 1 と 2 と 3 と 4 が 5 と互いに素(計4つ)
- φ(7) = 6 ← 1 と 2 と 3 と 4 と 5 と 6 が 7 と互いに素(計6つ)
というように、素数の場合はオイラー関数で 1つ少なく表されます。
p を素数とすると、
φ(p) = p – 1
になります。
【例】
- φ(5) = 5 – 1
- φ(5) = 4
フェルマーの小定理
先ほどのオイラー関数(φ(p) = p – 1)がフェルマーの小定理になるようです。
- フェルマー ← ピエール・ド・フェルマー(1607 – 1665)フランスの数学者。
フェルマーの最終定理とか大定理とか小定理があります。
いまいち用語の定義がわかりませんが、定理とは公理・定義だけから論理的に導き出せる(一般的)命題だそうです。
一言で説明すると以下のようになると思います。
- 公理 ← とにかく正しいということにする文章
- 定義 ← 議論を進めるための取り決め、主に言葉を決める
- 定理 ← 公理から導かれ定義された言葉で正しいことが証明できる文章
ネットを調べると(本当は学術書を読まないといけませんが)「フェルマー・オイラーの定理」とひとまとめになっていることもあります。
以下の場合
- p ← 素数
- a ← p と互いに素な整数
つまり、a と p は素数で、a と p は互いに素になります。
- φ(p) = p – 1 ← オイラーの定理(p が素数の時だけ使えます)
- a^p-1 ≡ 1(mod p) ← フェルマーの小定理
↑
このフェルマーの小定理を分かりやすく表示するとかずのようになります。
または、以下のように表示できます。
p が素数だとすると
φ(n) = p – 1 ← p が素数の時だけ使えます。
になるので、
は、以下のようになります。
実際に数値を入れて計算してみます。
p を 11 とすると以下のようになるので、確かに成立しています。
【例】
- 1^10 ≡ 1 ≡ 1(mod 11) ← 11 が素数
- 2^10 ≡ 1024 ≡ 1(mod 11) ← 11 × 93 + 1 = 1024 ← 11 が素数
- 3^10 ≡ 59049 ≡ 1(mod 11) ← 11 × 5368 + 1 = 59049 ← 11 が素数
p を素数とすると、
{1, . . , p-1} というように p は互いに素になります。
また、a は p と互いに素になります。
ここから
a, 2a, 3a, 4a, …., (p – 1)a は p と互いに素になります。
これを p で割った余りがすべて異なります。
【例】
- φ(5) = 4 ← 1 と 2 と 3 と 4 が 5 と互いに素
- φ(7) = 6 ← 1 と 2 と 3 と 4 と 5 と 6 が 7 と互いに素
これより、a を 5、p を 7 で試してみると
- a ← 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55
- p ← 5, 3, 1, 6, 4, 2, 0, 5, 3, 1, 6 ← 0 ~ 6 までの数が1個ずつ出てくる。
※0 ~ 6 までであることに注意。これが繰り返えされます。
例えば、
a × 2a × 3a ×・・・× (p – 1)a
≡1 × 2 × 3 × 4 × ・・・× (p – 1)
上の p で確認したように、順番は昇順、降順ではないが、すべての数字が出てきます。
例えば、p が 7 なら 1 ~ 6 まで全部出てきます。
ここから「階乗(かいじょう)」で表現できます。
- 階乗 ← 1 から n までのすべての整数の積を言います。
【例】
例えば、p を 11 とすると、階乗は以下のようになります。
10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 3,628,800
また、a を 5、p を 7 で試してみると
(5 × 1)(5 × 2)(5 × 3)(5 × 4)(5 × 5)(5 × 6) ≡ 6!(mod 7)
a^(p-1) × (p – 1)! ≡ (p – 1)! (mod p) なので、
(5^6) × (6!) ≡ 6!(mod 7) となり、
6! と 7 は互いに素なので、左辺と右辺を 6! で割ることができます。
そうすると、
5^6 ≡ 1(mod 7)
になります。
実際に計算してみると、
5^6 = 15,625 となり、
15,625 = 2232 × 7 + 1 となり、確かに
5^6 ≡ 1(mod 7)
になりました。
ここより
a^p-1 ≡ 1(mod p)
となります。
【例】
5^72 ≡ 1(mod 73)
- 73 は素数
- 72 は 73 から 1 引いた数
- 5 は 73 と互いに素
RSA暗号
ようやくここまで来ました。
今まで、勉強してきた数学の知識を使って、実際に RSA 暗号の計算を実践してみます。
①秘密鍵を作る
秘密鍵は 2 の素数(p,q)で作ります。
- p = 5
- q = 11
②公開鍵を作る
公開鍵は n,e の 2 つの整数で作ります。
n = pq
n = 5 × 11 = 55
n は 55 になります。
e は (p – 1) と (q – 1) と互いに素となる数の中から適当に見つけます。
今回の場合は、
(p – 1) = 4
(q – 1) = 10
なので、4 と 10 と互いに素となる数を見つけます。
互いに素とは、2つの整数の公約数が「1」のみであることを言います。
例えば、2つの整数が 2 と 5 の場合は、公約数が「1」のみであると言えます。
公約数とは、ある数を割り切れる数のことを言います。
たとえば、8 と 10 の公約数は、1, 2 です。
上の場合は、4 と 10 との整数の公約数が「1」のみとなる整数を選ぶので
e = 3 とします。
→自分で決めるので(任意なので)、すでに決まっているわけではありません。
3 は、4 とも 10 とも整数の公約数は 1 しかありませんので互いに素となります。
その結果、公開鍵 (n, e) は (55, 3) に決まりました。
③メッセージを数字にする
メッセージを ASCII コードで数字にします。
今回は、数字「012」のメッセージを送ります。
数字「012」を ASCII コードにすると「48」「49」「50」になります。
※このメッセージの数字は、n よりも小さくする必要があります。今回の場合は n は 55 なので、55 以下の数字にする必要がります。n 以上にすると、時計の原理のように、1週回った数になることに注意です。
④公開鍵を使って暗号化する
メッセージ「48」「49」「50」を e 乗した数を n で割った余りを暗号文にします。
- n = 55
- e = 3
48^3 ÷ 55 の余り
110,592 mod 55 = 42
49^3 ÷ 55 の余り
117,649 mod 55 = 4
50^3 ÷ 55 の余り
125,000 mod 55 = 40
よって暗号文は、「42」と「4」と「40」になります。
「42」と「4」と「40」を ASCII コードで表すと「*」、「EOT(転送終了)」、「(」 になります。
⑤暗号文を相手に送る
上記暗号文をメールや何かツールを使って相手に送ります。
⑥暗号文を数字にする
先ほどのメッセージ「*」、「EOT(転送終了)」、「(」を ASCII コードより数字にします。
以下のようになります。
暗号文:「42」と「4」と「40」
⑦ L の値を求める
L は RSA の暗号化にも復号にも使いません。
鍵ペアを作成するときに利用します。
L は (p – 1) と (q – 1) の最小公倍数です。
L = (p – 1) と (q – 1) の最小公倍数
今回の場合は、
L = LCM(p – 1, q – 1) = LCM(4, 10) = 20
- 4 ← 4, 8, 12, 16, 20, 24, 28, 32
- 10 ← 10, 20, 30, 40, 50, 60
4 と 10 の最小公倍数は、20 です。
L = 20 になります。
↑
この 20 は秘密鍵を持っている人しか計算できません。
⑧ d の値を求める
de – yL = 1 の場合の(d, y)を求めます。
これを式にすると以下のようになります。
de – yL = 1 ← 一次不定方程式
e = 3
L = 20
3d – 20y = 1 ← 一次不定方程式になります。
ちなみに、不定方程式なので、解は無数にあります。
また、3 と 20 は互いに素なので、1 が解として可能です。
ユークリッドの互除法を利用します。
ユークリッドの互除法を利用して最大公約数を見つけます。
20 = 3 × 6 + 2
3 = 2 × 1 + 1
2 = 1 × 2 + 0
最後に割る数が最大公約数になります。
上の場合は 1 です。
d と y を導き出すには上で利用した式を利用します。
上の式
①20 = 3 × 6 + 2
↓
②3 = 2 × 1 + 1
↓
③2 = 1 × 2 + 0
②の式から 1 を導き出します。
3 = 2 × 1 + 1 ← これを変形します。
1 を 左辺にもっていき、2 × 1 を右辺にもっていきます。
1 = 3 – (2 × 1)
この 2 の部分に①の式を入れます。
①の式 20 = 3 × 6 + 2 を以下のように変えます。
2 = 20 – (3 × 6)
この式を 1 = 3 – (2 × 1) の 2 の部分に入れます。
1 = 3 – ((20 – (3 × 6)) × 1)
1 = 3 – (20 × 1) – (3 × 6)
3 が重複しているのでカッコから出してまとめます。
1 = – (20 × 1) + (3 × 7)
ここから
3d – 20y = 1
(d, y) = (7, 1) となります。
7 と 1 は、自然数解となります。
自然数とは正の整数のことを言います。
例えば、1,2,3,4,5,6,7… となります。
⑨復号する
メッセージ:「48」「49」「50」
暗号文:「42」と「4」と「40」
復号の仕方は、暗号文を d 乗して n で割ります。
d:7
n:55
42^7 mod 55 = 48
4^7 mod 55 = 49
40^7 mod 55 = 50
以上、復号ができました。
参考サイト・図書
第1回 余りつき割り算
第2回 合同式の計算方法
第3回 合同式の演習
第4回 ユークリッドの互除法と一次不定方程式
第5回 合同式の重要性質2(乗法単元)
第6回 中国剰余定理
第7回 フェルマーの小定理
第8回 RSA暗号の仕組み解説
第9回 RSA暗号の仕組み[証明]


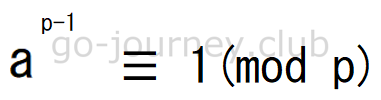

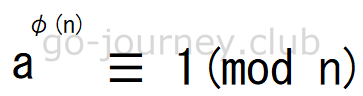







コメント